1. Означення визначника. Основні властивості визначників.
Властивості визначника:
- Визначник не зміниться, якщо його рядки замінити відповідними стовпцями.
- Якщо переставити місцями два рядки (стовпці), то визначник змінить знак.
- Якщо 1 з рядків (стовпців) визначника складається тільки з нулів, то визначник дорівнює 0.
- Якщо визначник має 2 однакових рядки (стовпці), то він дорівнює 0.
- Спільний множник, що міститься в усіх елементах 1 рядка (стовпця), можна винести за знак визначника.
- Якщо у визначнику елементи 2 рядків (стовпців) пропорційні, то визначник дорівнює 0.
- Якщо кожен елемент n-го рядка (стовпа) є сумою двох доданків, такий визначник дорівнює сумі 2 визначників, у 1 з яких n-ий рядок (стовп) складається з перших доданків, а у 2 – з других; інші елементи всіх трьох визначників однакові.
- Визначник не зміниться, якщо до елементів 1 рядка (стовпця) додати відповідні елементи іншого рядка (стовпця), помножені на 1 й те саме число.
2. Мінор. Алгебраїчне доповнення елемента визначника.
Мінором Mij елемента aij визначника називається визначник, який утворюється ви кресленням i-го рядка і j-го стовпця. Алгебраїчним доповненням Aij елемента aij називається його мінор, взятий зі знаком (-1)i+j. Визначник дорівнює сумі добутків елементів якого-небудь рядка (стовпця) на їхні алгебраїчні доповнення. Сума добутків елементів будь-якого рядка (стовпця) на алгебраїчні доповнення відповідних елементів іншого рядка (стовпця) дорівнює 0.
3. Довести, що визначник дорівнює сумі добутків елементів будь-якого рядка (стовпця) на їх алгебраїчне доповнення.
4. Довести, що сума добутків елементів будь-якого рядка (стовпця) на алгебраїчне доповнення відповідних елементів іншого рядка (стовпця) дорівнює нулю.
5.Визначення матриці. Дії над матрицями. Обернена матриця.
Прямокутна таблиця чисел складена з m рядків і n стовпців і записана у вигляді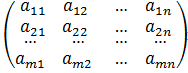 називається матрицею. Сумою двох матрицьоднакового розміру Аmxn і Вmxnназивається матрицяСmxn=(cij)=(aij+bij). Добутком матриці на число k називається матриця B=kA=(kaij). Різниця двох матриць однакового розміру визначається як сума матриці А і матриці В, помноженої на (-1). Матриця А називається узгодженою з матрицею В, якщо кількість стовпів матриці А дорівнює кількості рядків матриці В. Якщо матриця А узгоджена з матрицею В, то їх добутком називається матриця, у якої елемент aij дорівнює сумі добутків елементів i-го рядка матриці А на відповідні елементи j-го стовпця матриці В. Матриця А* називається транспонованою до матриці А, якщо a*ij=aji. Матриця А-1 називається оберненою до матриці А, якщо АА-1=Е (одиничній матриці). Для існування оберненої матриці необхідно, щоб матриця А була не виродженою (визначник не дорівнює 0).
називається матрицею. Сумою двох матрицьоднакового розміру Аmxn і Вmxnназивається матрицяСmxn=(cij)=(aij+bij). Добутком матриці на число k називається матриця B=kA=(kaij). Різниця двох матриць однакового розміру визначається як сума матриці А і матриці В, помноженої на (-1). Матриця А називається узгодженою з матрицею В, якщо кількість стовпів матриці А дорівнює кількості рядків матриці В. Якщо матриця А узгоджена з матрицею В, то їх добутком називається матриця, у якої елемент aij дорівнює сумі добутків елементів i-го рядка матриці А на відповідні елементи j-го стовпця матриці В. Матриця А* називається транспонованою до матриці А, якщо a*ij=aji. Матриця А-1 називається оберненою до матриці А, якщо АА-1=Е (одиничній матриці). Для існування оберненої матриці необхідно, щоб матриця А була не виродженою (визначник не дорівнює 0). 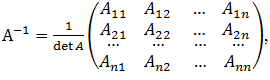 , де Аij – алгебраїчні доповнення елементів aij визначника матриці А.
, де Аij – алгебраїчні доповнення елементів aij визначника матриці А.
6. Система лінійних рівнянь. Вивести формули Крамера.
СЛР називається однорідною, якщо всі вільні члени дорівнюють 0, і неоднорідною, якщо хоч один не дорівнює 0. Упорядкований набір чисел називається розв’язком СЛР, якщо при підстановці цих чисел замість невідомих всі рівняння системи перетворяться в тотожності. СЛР називається сумісною, якщо вона має хоч 1 розв’язок, несумісною, якщо розв’язків немає. Сумісна СЛР, яка має єдиний розв’язок називається визначеною, якщо розв’язків більше 1, то невизначеною, а множина її розв’язків називається параметричною. 2 СЛР є еквівалентними, якщо вони мають 1 і ту ж множину розв’язків.
7. Матричний запис системи лінійних рівнянь та її розв'язок.
Нехай матриця Х – матриця невідомих, В – матриця вільних членів, тоді СЛР можна записати 1 матричним рівнянням: АХ=В. Якщо матриця А має обернену матрицю А-1, то Х=А-1В.
8. Вектори. Лінійні операції над векторами. Скалярний добуток векторів.
Вектор – напрямлений відрізок. Координати вектора: (х1-х2; у1-у2). Довжина вектора 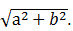 . Вектори, які лежать на паралельних прямих називаються колінеарними. Вектори, які лежать на паралельних площинах називаються компланарними. Вектори називаються рівними, якщо вони колінеарні, однаково напрямлені і рівні за модулем. Вектор, колінеарний даному вектору, рівний йому за модулем і протилежно напрямлений, називається протилежним. Сума двох векторів – вектор, напрямлений з початку вектора а в кінець вектора b, за умови, що початок вектора b збігається з кінцем вектора а (за правилом трикутника). Сума кількох векторів – вектор, який замикає ламану, побудовану з даних векторів. Різницю векторів а і b розглядають як суму векторів а і –b. Добутком дійсного числа α на вектор а є вектор с=αа, а напрям збігається з напрямом вектора а при α>0 і протилежний при α<0.Скалярний добуток векторів: |a|
. Вектори, які лежать на паралельних прямих називаються колінеарними. Вектори, які лежать на паралельних площинах називаються компланарними. Вектори називаються рівними, якщо вони колінеарні, однаково напрямлені і рівні за модулем. Вектор, колінеарний даному вектору, рівний йому за модулем і протилежно напрямлений, називається протилежним. Сума двох векторів – вектор, напрямлений з початку вектора а в кінець вектора b, за умови, що початок вектора b збігається з кінцем вектора а (за правилом трикутника). Сума кількох векторів – вектор, який замикає ламану, побудовану з даних векторів. Різницю векторів а і b розглядають як суму векторів а і –b. Добутком дійсного числа α на вектор а є вектор с=αа, а напрям збігається з напрямом вектора а при α>0 і протилежний при α<0.Скалярний добуток векторів: |a|
·|b|
·cosφ. Якщо вектори а і b перпендикулярні, то їх скалярний добуток дорівнює 0. Якщо 0≤ φ < π/2, то скалярний добуток більше 0. Якщо π/2 < φ ≤ π, то скалярний добуток менше 0.
9. Векторний базис на площині і в просторі.
Базисом на площині називається довільна упорядкована пара неколінеарних векторів. Базисом у просторі називається довільна упорядкована трійка некомпланарних векторів. Розкласти вектор за базисом означає зобразити його у вигляді лінійної комбінації базисних векторів. Якщо вектори a, b, c складають базис і вектор d розкладений за цим базисом, тобто d = αa+βb+γc, то числа α, β, γ називаються координатами вектора d в даному базисі, а вектори αa, βb, γc – компонентами вектора d. Кожен вектор, паралельний якій-небудь прямій, можна розкласти за базисом на цій прямій. Кожен вектор, паралельний якій-небудь площині, можна розкласти за базисом на цій площині. Кожен вектор можна розкласти за базисом у просторі. Координати вектора у кожному випадку визначаються однозначно.
10. Канонічне і параметричне рівняння прямої
Вектор s, паралельний прямій, називається направляючим вектором цієї прямої. Отже, нехай пряма l проходить через точку М1 (x1, y1, z1), що лежить на прямій паралельно вектору 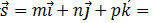
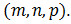 .Розглянемо довільну точку М (x, y, z) на прямій. З малюнка видно, що
.Розглянемо довільну точку М (x, y, z) на прямій. З малюнка видно, що 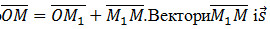 .Вектори і колінеарні, тому знайдеться таке число t, що , де множник t може приймати будь-яке числове значення в залежності від положення точки M на прямій. Множник t називається параметром. Позначивши радіус-вектори точок М1 і М відповідно через і , отримаємо . Це рівняння називається векторним рівнянням прямої. Воно показує, що кожному значенню параметра t відповідає радіус-вектор деякої точки М, що лежить на прямій.
.Вектори і колінеарні, тому знайдеться таке число t, що , де множник t може приймати будь-яке числове значення в залежності від положення точки M на прямій. Множник t називається параметром. Позначивши радіус-вектори точок М1 і М відповідно через і , отримаємо . Це рівняння називається векторним рівнянням прямої. Воно показує, що кожному значенню параметра t відповідає радіус-вектор деякої точки М, що лежить на прямій.
Отримані рівняння називаються параметричними рівняннями прямої.При зміні параметра t змінюються координати x, y і z і точка М переміщається по прямій.
Вектори і колінеарні, тому їх відповідні координати повинні бути пропорційні, отже, –канонічнірівняння прямої.
11.Рівняння прямої, що проходить через дану точку і перпендикулярно даному вектору.
Скалярний добуток перпендикулярних векторів дорівнює 0. Отже, A(x-x0)+B(y-y0)=0 – рівняння прямої, яка проходить через точкуM0(x0; y0) перпендикулярно до нормального вектораn=(A; B). Цей вектор називається нормальним вектором прямої. Пряма має безліч нормальних векторів. Усі вони паралельні, отже, їхні відповідні координати пропорційні.
12.Загальне рівняння прямоїта його частинні випадки.
Рівняння Ax+By+C=0 називається загальним рівнянням прямої на площині, А і В – координати вектора нормалі до прямої; С – вільний член:
С=0 – рівнянняAx+By=0 визначає пряму, що проходить через початок координат;
В=0, А≠0, С≠0 – рівнянняAx+С=0 визначає пряму, паралельно осі Ох;
В=0, А≠0, С=0 – рівняння Ax=0 визначає пряму, яка співпадає з віссю Ох;
А=0, В≠0, С≠0 – рівняння By+С=0 визначає прямупаралельно осі Оу;
А=0, В≠0, С=0– рівняння Ву=0 визначає пряму, яка співпадає з віссю Оу;
А=0, В=0, С=0 – рівняння визначає пряму y=kx+b з кутовим коефіцієнтом.
13.Коло. Рівняння кола.
Коло – множина точок площини, відстані яких від заданої точки площини дорівнюють сталому числу (радіусу). Рівняння (х-х0)2+(у-у0)2=R2 визначає коло з центром в точці С(х0, у0) і радіусом R. Якщо центром кола є початок координат, то рівняння кола має вигляд х2+у2=R2.
14. Взаємнерозміщення двох прямих. Кут між двома прямими.
Кутом між прямими а1 і а2 називається кут ϴ, на який треба повернути пряму а1 (проти годинникової стрілки), щоб вона сумістилася з прямою а2. Якщо прямі задано канонічними рівняннями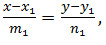
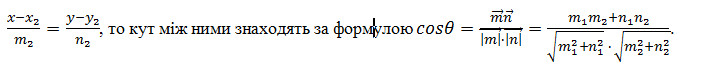
Умовою паралельності прямих є пропорційність координат напрямних векторів 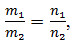 , а умовою перпендикулярності – рівність .
, а умовою перпендикулярності – рівність .
Якщо прямі задано рівняннями з кутовим коефіцієнтом, то . Ознакою паралельності цих прямих буде рівність їх кутових коефіцієнтів, а ознакою перпендикулярності – рівність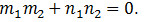 .
.
Якщо прямі задано загальними рівняннями,то . Ознакою паралельності цих прямих є рівність , а перпендикулярності – рівність .
15. Еліпс. Канонічне рівняння еліпса.

16. Дослідженняформи еліпса по його канонічному рівнянню.

17. Гіпербола.Канонічне рівняння гіперболи.

18. Дослідження форми гіперболи по його канонічному рівнянню.
19. Парабола. Канонічне рівняння параболи.
Парабола – множина всіх точок площини, кожна з яких знаходиться на однаковій відстані від даної точки, яка називається фокусом і від даної прямої, яка називається директрисою і не проходить через фокус. Канонічне рівняння параболи у2=2рх; p>0 – параметр параболи; точкаF (p/2;0) – фокус параболи. Пряма х=-р/2 – директриса параболи; r= x+p/2 – фокальний радіус точки М(х; у). Рівняння параболи х2=2ру. Ексцентриситет параболи ε=1.
20. Дослідження форми параболи по його канонічному рівнянні.
21.Загальне рівняння площини та його дослідження.
Ax+By+Cz+D=0 – загальне рівняння площини; – нормальний вектор; Ax+By+Cz=0 – рівняння площини, що проходить через точку О(0; 0; 0); Ax+By+D=0–рівняння площини, паралельної осі Oz; Ax+By =0 – рівняння площини, що проходить через вісьOz; Ax +D=0 – рівняння площини, паралельної площині Oуz; A(x-х0)+B(y-у0)+C(z-z0)=0 –рівняння площиниP, що проходить через точку М0(х0; у0; z0)і має нормальний вектор .
22. Рівнянняплощини, що проходить через три точки. Кут між двома площинами. Умови паралельності і перпендикулярності двох площин. Відстань від точки до площини.

23. Функція. Границя функції.
Якщо кожному числу х з деякої множиниD за певним правилом поставлене у відповідність єдине число у, то у є функцією від х. Область визначення функції – множинаD значень аргументу х, для яких функція y=f(x) має дійсний зміст. Область значень функції – множина Е всіх чисел у, таких, щоy=f(x). Функція є парною, якщо f(-x)=f(x), і непарною, якщо f(-x)=-f(x). Функція, яка визначена на всій числовій прямій, є періодичною. Якщо при х1<х2:
- f(х1)<f(х2), то функція є зростаючою;
- f(х1)>f(х2), то функція є спадною;
- f(х1)≤f(х2), то функція є неспадною;
- f(х1)≥f(х2), то функція є незростаючою;
Якщо для довільної послідовності точок взятої з області визначення відповідна послідовність значень функції збігається до того самого числа, то це число називають границею функції в точці.
24. Нескінченновеликі і малі функції. Основні властивості нескінченно малих величин. Основні теореми про границі.

Властивості:
- Для того, щоб число А було границею функції f(x) при х→х0, необхідно, щоб різниця f(x)-А була нескінченно малою величиною.
- Якщо функція α(х) – нескінченно мала величина при х→х0, то функція 1/α(х) є нескінченно великою величиною при х→х0, і навпаки, якщо β(х) – нескінченно велика величина при х→х0, то 1/β(х) є нескінченно малою величиною при х→х0.
- Сума скінченного числа нескінченно малих величин є величина нескінченно мала.
- Добуток обмеженої функції на нескінченно малу є величина нескінченно мала.
- Частка від ділення нескінченно малої величини на функцію, яка має відмінну від нуля границю, є величина нескінченно мала.
Основні теореми про границі:
- Для того, щоб послідовність мала границю, треба, щоб xn=a+yn, де yn – нескінченно мала послідовність.
- Якщо кожна з функцій f(x) iφ(x) має скінченну границю в точці х0, то в цій точці існують також границі функцій f(x)±φ(x), f(x)
·φ(x), f(x)/φ(x).
- Якщо границя справа дорівнює границі зліва, то точка посередині матиме ту саму границю.
- Якщо значення функції ≥0, то значення границі теж буде ≥0.
- Якщо φ(х) монотонна і обмежена при х<х0 або х0<х, то існує відповідно її ліва або права границя.
25.Числова послідовність. Границя послідовності.
Якщо кожному натуральному n є N числу за певним правилом ставиться у відповідність число xn, то множину чисел {x1, x2, …, xn, …} називають послідовністю.Число х0 є границею послідовності {xn}, якщо для довільного числа ε>0 існує такий номер N=N(ε), що при всіхn>N виконується нерівність |xn-x0|<ε.
Послідовність з границею збіжна, без границі – розбіжна.
26.3адача, що приводить до поняття похідної.
Задача про швидкість прямолінійного руху. За час Δt (приріст часу)рухома точка пройде шлях ΔS (приріст шляху). За часt+Δt матеріальна точка пройде шляхS(t)+ΔS = S(t+Δt), томуΔS=S(t+Δt)-S(t).Середня швидкість руху точки за проміжок часу – відношення приросту шляху до приросту часу: υc = ΔS/Δt = = (S(t+Δt)-S(t))/Δt.
27. Означення похідної. Механічний, фізичний та геометричний зміст похідної.
Похідна – границя відношення приросту функції до приросту аргументу.
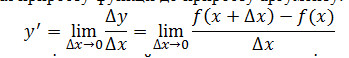
Механічний зміст похідної: швидкість в даний момент часу – похідна від пройденого шляху S(t) за часомt:υ=S’(t).
Фізичний зміст похідної: Похідна від шляху за часом дорівнює миттєвій швидкості руху матеріальної точки.
Геометричний зміст похідної: кутовий коефіцієнт дотичної до кривої y=f(x)в точці М0(х0; у0)або тангенс кута α, що утворює дотична до кривої в даній точці з додатним напрямом осі Ох, - це похідна f’(х0) в цій точці.
28. Рівняння дотичної до графіка функції в точці. Нормаль до графіка функції
29. Вивестиформулу для знаходження похідної суми (різниці) двох функцій.
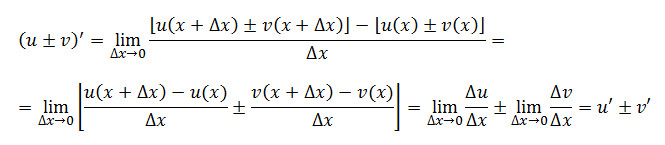
30. Вивестиформулу для знаходження похідної добутку двох функцій.
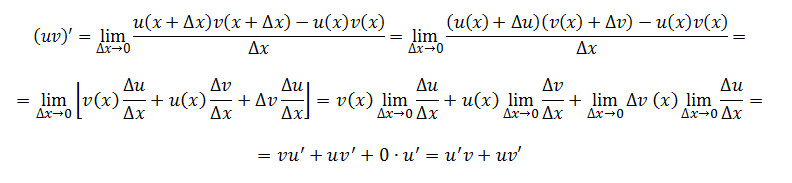
31. Вивестиформулу для знаходження похідної частки двох функцій.
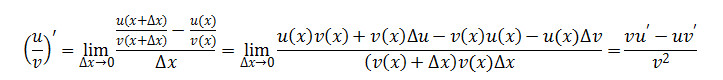
32. Похіднатригонометричних функцій. Довести, що (sinх)’=cosx.
33. Монотонністьфункції. Локальний екстремум функції.
34.Опуклість і вгнутість кривих. Точки перетну графіка функції.
35. Асимптоти кривої.
36. Схема дослідження функції.
- Знаходження ОДЗ функції
- Дослідження функції на парність/непарність
- Визначення точок перетину з віссю абсцис та віссю ординат
- Знаходження похідної функції
- Значення похідної в точці 0
- Розбиття критичними точками ОДЗ
- Побудова таблиці
37. Первісна.Невизначений інтеграл.
ФункціяF(x) називається первісною функції на проміжку (a; b), якщоF(x) диференційована на (a; b) іF’(x)=f(x) для всіхx є (a; b).
Множина {F(x)+C} всіх первісних функціїf(x) називається невизначеним інтегралом функціїf(x) на цьому проміжку. , якщо F’(x)=f(x).
38.Основні властивості невизначеного інтеграла.
- Похідна від невизначеного інтеграла дорівнює підінтегральній функції
- Невизначений інтеграл від диференціала деякої функції дорівнює сумі цієї функції і довільної сталої
- Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу
- Сталий множник можна винести за знак інтеграла
- Невизначений інтеграл від суми двох функцій дорівнює сумі інтегралів від цих функцій
39. Методиінтегрування невизначеного інтеграла.

40.3адача, що приводить до поняття визначеного інтеграла. Означення визначеного інтеграла. Властивості визначеного інтеграла.
Задача про площу криволінійної трапеції: …
Визначений інтеграл — це інтеграл функції з вказаною областю інтегрування. Формула Ньютона-Лейбніца:
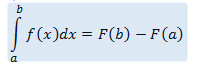
Властивості:
- Визначений інтеграл з однаковими межами інтегрування дорівнює 0.
- Від перестановки меж інтегрування інтеграл змінює знак на протилежний.
- Сталий множник С можна винести за знак визначеного інтеграла.
- Інтеграл від суми дорівнює сумі інтегралів.
- Якщо функція f(x) неперервна на відрізку [a; b], та на цьому відрізку знайдеться така точка с, що
41.Методи інтегрування визначеного інтеграла.
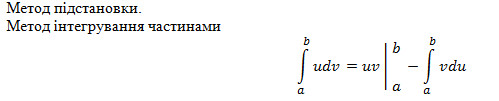
42. Обчислення площ плоских фігур. Приклади.
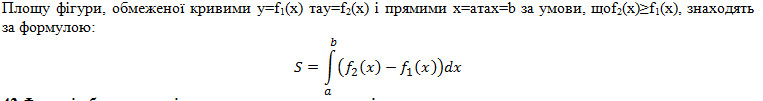
43.Функція багатьох змінних: визначення, символіка.
Якщо кожній парі чисел (x, y) єD за певним законом відповідає числоz, то кажуть, що на множиніD визначено функціюz від двох змінних х і у і записують z=f(x, y).
44.Частинні похідні першого, другого і третього порядку функції багатьох змінних.
Якщо існує границя 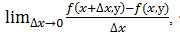 , то вона називається частинною похідною функціїz=f(x, y) в точціM(x; y) по змінній х.
, то вона називається частинною похідною функціїz=f(x, y) в точціM(x; y) по змінній х.
Частинними похідними другого порядку функцій z=f(x, y) називаються їх частинні похідні від частинних похідних першого порядку. Аналогічно означаються похідні вищих порядків.
45. Диференційованістьфункції багатьох змінних. Повний диференціал функції багатьох змінних.
46. Поняттяпро сукупність розв'язків, загальний та частинний розв'язок диференціального рівняння. Задача Коші.
Диф. рівнянням першого порядку називається рівняння виду F(x, y, y’), яке пов’язує незалежну змінну х, невідому функціюy=y(x) та її похідну.
Розв’язком диф рівняння називається диференційована на цьому інтервалі функція у=φ(х), яка при підстановці в рівняння перетворює його в тотожність по х на (a; b). Частинним розв’язком рівняння називається функція, яка утворюється із загального розв’язку у=φ(х, С) при певному значенні сталої С=С0.
Задача Коші — одна з основних задач теорії диференціальних рівнянь полягає в пошуку розв'язку (інтеграла) диференціального рівняння, що задовольняє початковим умовам
47. Диференціальнірівняння першого порядку з відокремлюваними змінними, алгоритм їх розв'язку.
Рівняння виду y’=f(x)φ(y), деf(x) іφ(y) – задані і неперервні не деякому інтервалі функції, називаються диф рівняннями з відокремленими змінними.
48.Однорідні диференціальні рівняння першого порядку. Їх розв'язок у загальному вигляді.
Функція f(x, y) називається однорідною функцією n–го виміру відносно змінних х та у, якщо для довільного числаt≠0 виконується тотожністьf(tx, ty)=tnf(x, y). Диф рівнянняy’=f(x, y) називається однорідним, якщо функціяf(x, y) є однорідною функцією нульового виміру.
49. Лінійні диференціальні рівняння першого порядку: алгоритми їх розв’язку.
Лінійним диф рівнянням першого порядку називається рівняння виду y’=p(x)y=f(x), деp(x)іf(x) – задані і неперервні на деякому проміжку функції.
50. Диференціальнірівняння другого порядку. Найпростіші диференціальні рівняння другого порядку: алгоритм їх розв'язку.
51. Розв'язоклінійного однорідного диференціального рівняння другого порядку з постійними коефіцієнтами у випадку, якщо корені характеристичного рівняння дійсні і різні.
52. Розв'язоклінійного однорідного диференціального рівняння другого порядку з постійними коефіцієнтами у випадку, якщо корені характеристичного рівняння комплексні.
53. Визначеннячислового ряду. Приклади. Збіжні та розбіжні числові ряди.
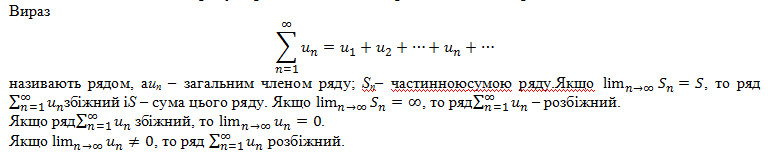
54. Властивостічислових рядів: довести теореми.
- Збіжний ряд можна множити почленно на 1 й те саме число.
- Збіжні ряди можна почленно додавати і віднімати.
- На збіжність ряду не впливає відкидання або приєднання до нього скінченної кількості членів.
- Ряд збіжний (розбіжний) тоді, коли збіжний (розбіжний) довільний його залишок.
55. Довести,якщо ряд збіжний, то його загальний член прямує до нуля.
56. Рядиз невід’ємними членами. Ознаки збіжності рядів з невід’ємними членами.

57. Степеневий ряд. Теорема Абеля.
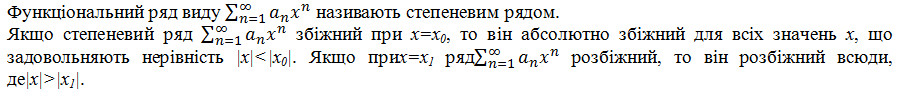
58.Інтервал та радіус збіжності степеневого ряду.

59. Ряд Тейлора.
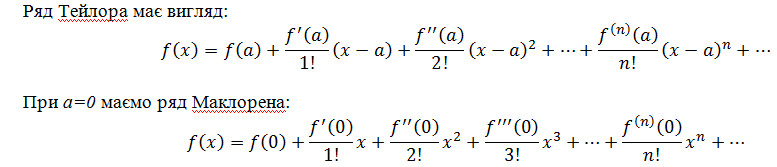
60. Означення комплексного числа. Властивості операцій над комплексними числами (доведення).
Комплексне число – вираз z=a+bi, де aі b– дійсні числа, аi – уявна одиниця (i2=-1).a – дійсна частина,b – уявна частина.Дії над комплексними числами:
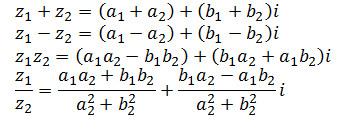
Арифметичні дії над комплексними числами виконуються за звичайними правилами дій над двочленами.
61. Комплексна площина. Модуль та аргумент комплексного числа.
Комплексне число відображається на площині точкою М(a; b) або вектором ОМ. Така площина умовно називається комплексною площиною змінної z, вісь Ох – дійсною віссю, а Оу – уявною.Модуль комплексного числа: . Аргумент комплексного числа:tgφ=b/a.
62. Комплекснастепінь числа е. Властивості комплексного степеня (доведення).
63. Алгебраїчната тригонометрична форми запису комплексного числа. Множення та ділення
комплексних чисел, записаних в тригонометричній формі (доведення).
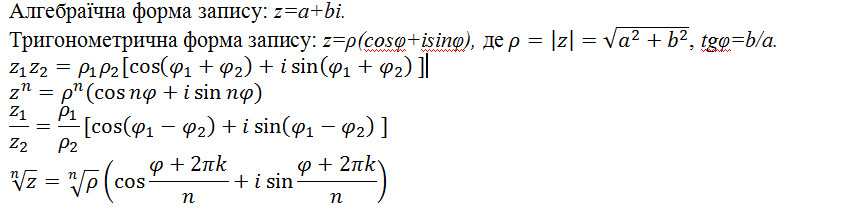
64. Показниковаформа запису комплексного числа. Множення та ділення комплексних чисел, записаних в показниковій формі.
Формула Ейлера: eiφ=cosφ+isinφ.
Показникові форма запису: z=ρeiφ.